Interactive Session 4

1. Learning from existing functions

Function documentation

Let’s check out documentation for a few basic functions in R. This will help us get an idea of the type of features we may want to add to our functions in the future, and to familiarize ourselves with how to read and understand function documentation (which can admittedly be…a lot).

In R…

To see documentation for R functions, run ?functionname. This should bring up the function documentation in the Help tab in RStudio. For example, try running ?min.

What are the different pieces in the documentation?

Description: gives an overview of what the function does
Usage: shows general usage and default behaviors
Arguments: the arguments…
Details: any other details…
Value: information about the output returned
Examples: selected examples (but also…Google it)

In Python…

To see function documentation in Python, run help(functionname). This will bring up a new window with information about the function (press q to escape). For example, try running help(min) in the Python interpreter.

2. Basic pieces of a function

Components of a function

From Chapter 19 - Functions in R for Data Science: “There are three key steps to creating a new function:

You need to pick a name for the function.
You list the inputs, or arguments, to the function inside function.
You place the code you have developed in body of the function.”

3. Getting started - function examples in R & Python

Example 1 (from lecture slides)

The bird-dog sum example in R:

birddog_sum <- function(bird, dog) {
  pets = bird + dog
  return(pets)
}

# Use it! 
birddog_sum(bird = 2, dog = 5)

[1] 7

The bird-dog sum example in Python:

def birddog_sum(bird, dog):
  pets = bird + dog
  return(pets)
  
birddog_sum(bird = 10, dog = 99)

Note the similarities and differences in syntax between R and Python functions.

Example 2

Make a function called double_it that doubles any value input value.

In R:

# Create the function: 
double_it <- function (x) {
  print(2 * x)
}

# Try it out! 
double_it(24)

[1] 48

# And on a vector, still works: 
double_it(c(1, 0.5, -200))

[1]    2    1 -400

In Python:

import numpy as np

def double_it(x):
  print(2 * x)
  
double_it(25)

# Create a vector (NumPy array)
v = np.array([4, 1])

# Use the function to double all elements in the vector: 
double_it(v)

[8 2]

# Question: what if you apply double_it() to a LIST in Python? 
w = [3,5,8]

double_it(w) # Note this behavior - lists & tuples are operated on differently than NumPy arrays / vectors!

[3, 5, 8, 3, 5, 8]

Example 3

Write a function that returns the statement “I am ___ years old!”, where the blank is entered by the user as argument age.

In R:

exclaim_age <- function(age) {
  print(paste("I am", age, "years old!"))
}

exclaim_age(age = 10)

[1] "I am 10 years old!"

In Python:

def exclaim_age(age):
  print("I am", str(age), "years old!")
  
exclaim_age(age = 2)

I am 2 years old!

`print()` versus `return()`

What’s the difference between print() and return()?. The print() function just makes something visible to us. It does not get stored for later use. If we want an output to be stored for use, we use return().

What?

Yeah the difference can be kind of tricky, because it sometimes seems like when we use print() it has stored something. Let’s check out an example that highlights the difference.

Example 4

A Python example:

def find_max(val_1, val_2):
  if (val_1 > val_2):
    return(val_1)
  elif (val_2 > val_1):
    return(val_2)

# We can use that returned output for another calculation: 
5 * find_max(7, 3)

What happens if instead of return() we’d used print() here?

def find_max(val_1, val_2):
  if (val_1 > val_2):
    print(val_1)
  elif (val_2 > val_1):
    print(val_2)
  
# And when we try to use output for something else: 
5 * find_max(7, 3)

4. Functions with conditionals

Similar to for loops, we can have conditionals within functions - this means that what the function does with arguments will change based on what those argument values are.

Example

Returning to an example that we saw previously, let’s say we want to make a function that returns the age of an animal in animal years, given the species and age in human years. For example: 1 human year = 7 dog years, and 1 human year = 4.7 goat years.

Write a function with two arguments: animal and age, which converts the animal’s age from human to animal years.

In R:

animal_age <- function(animal, age) {
  if (animal == "dog") {
    print(age * 7)
  } else if (animal == "goat") {
    print(age * 4.7)
  } 
}

# Try an 8 year old dog.
animal_age(animal = "dog", age = 8)

[1] 56

# Try a cow & see what is returned. What happens? Consider.
animal_age(animal = "cow", age = 12)

# Try a dog that is "yellow" years old:
# animal_age(animal = "dog", age = "yellow")

Critical thinking

What if the input isn’t dog or goat? Remember this question - we’ll return to it later on.

A question to keep in mind: it’s easy enough to manually code in the animal species and conversion factor since we only have two animals. Would we want to manually write this out if we had 20 species? 50 species?

In Python:

def animal_age(animal, age):
  if (animal == "dog"):
    print(age * 7)
  elif (animal == "goat"):
    print(age * 4.7)
    
animal_age(animal = "dog", age = 15)

Example

Let’s say we have a table of the dogs’ favorite foods.

# A tibble: 4 × 2
  dog_name food      
  <chr>    <chr>     
1 Khora    everything
2 Teddy    salmon    
3 Waffle   pancakes  
4 Banjo    chicken

Write a function that only requires the dog name as an input, then automatically pulls information from the data frame (stored as dog_choice) to return the phrase “My name is _____ and I love eating ____!”

Here I’ll introduce a new function: dplyr::filter(). This is a fantastic function for creating subsets from our data. We’re going to be using it a LOT in our data wrangling lessons last week. For now, know that it returns a logical TRUE or FALSE based on whether or not elements in a vector satisfy the conditions.

Let’s talk through what this code is actually doing:

dog_menu <- function(name) {
  my_sub <- dplyr::filter(dog_choice, dog_name == name)
  print(paste("My name is", my_sub$dog_name, "and my favorite food is", my_sub$food))
}

# Try it! What is Waffle's favorite food?
dog_menu(name = "Waffle")

[1] "My name is Waffle and my favorite food is pancakes"

# And Khora? 
dog_menu(name = "Khora")

[1] "My name is Khora and my favorite food is everything"

Aha - now we can see that we don’t have to write out every value in our function! We can pull elements directly from a table to switch parameters based on user selection / inputs!

5. Functions meet for loops

Sometimes, we’ll want to iterate over different elements of a data structure (e.g. data frame columns), applying a function we write to each of them. We’ve learned a couple of coder-friendly tools to loop over columns (e.g. apply, purrr::map()), but let’s write one from scratch first.

Example

Write a function that iterates over each column in a data frame (name gets specified), calculating the mean value for each and returning the phrase “The mean value of (column name) is _____.”

Note: the colnames() function in base R returns column names.

df_means <- function(df) {
  for (i in 1:ncol(df)) {
    col_mean <- mean(df[[i]])
    column_name <- colnames(df[i])
    print(paste("The mean value of", column_name, "is", col_mean))
  }
}

df_means(df = mtcars)

[1] "The mean value of mpg is 20.090625"
[1] "The mean value of cyl is 6.1875"
[1] "The mean value of disp is 230.721875"
[1] "The mean value of hp is 146.6875"
[1] "The mean value of drat is 3.5965625"
[1] "The mean value of wt is 3.21725"
[1] "The mean value of qsec is 17.84875"
[1] "The mean value of vs is 0.4375"
[1] "The mean value of am is 0.40625"
[1] "The mean value of gear is 3.6875"
[1] "The mean value of carb is 2.8125"

Critical thinking

Why only the single square brackets to refer to the column names here? Try it! What is returned when we use colnames(mtcars[2]) versus colnames(mtcars[[2]])?

So, will this actually work on other data frames? Let’s make one!

the_fish <- tribble(
  ~brown, ~rainbow, ~cutthroat,
  16.2, 12.1, 21.9,
  24.7, 14.6, 18.3,
  12.1, 15.4, 30.2,
  10.4, 11.8, 26.3
)

df_means(df = the_fish)

[1] "The mean value of brown is 15.85"
[1] "The mean value of rainbow is 13.475"
[1] "The mean value of cutthroat is 24.175"

6. Adding helpful error and warning messages

We now know a bit about writing functions. But we also want them to be as helpful as possible - meaning that we need to create useful error messages, documentation and tests. We’ll start by adding some stop() statements to create error messages.

First, it’s important when designing a function to think about what will make it fail. For example, if a function does an age conversion on a number, what happens if the user inputs a character? What happens if a user only enters one argument value, but the function requires two? Let’s take a look at some examples for adding error messages.

Adding error messages with conditional checks + `stop()`

Returning to our function to convert animal ages:

animal_age <- function(animal, age) {
  if (animal == "dog") {
    print(age * 7)
  } else if (animal == "goat") {
    print(age * 4.7)
  }
}

We want to add some error messages that are helpful to the user of the function. We’ll use the stop() function

animal_age_stop <- function(animal, age) {
  
  if (!animal %in% c("dog", "goat")) {
    stop("Oops! Animal must be a dog or a goat.")
  }
  
  if (is.numeric(age) == FALSE) {
    stop("The age must be a number between 0 and 100")
  }
  
  if (age <= 0) {
    stop("Age must be a number greater than zero.")
  }
  
  if (animal == "dog") {
    print(age * 7)
  } else if (animal == "goat") {
    print(age * 4.7)
  }
}

Adding warning messages

Sometimes, you still want code to run (i.e., not throw an error message and stop), but there might be something suspicious about the inputs or outputs that you’d want to alert the user about. For example, maybe you’ll flag an input for dog age if the person adds a value over 22 years - it won’t not work, but it’ll give a friendly heads up that that’s a very old dog, are you sure that’s the value you wanted to enter?

We can add warning messages to functions in R using warning(). Keep in mind that the function will still run - this is very different than a hard stop from an error message.

Example: Betz’ Limit

The full power in wind hitting a turbine is:

\[P = 0.5\rho Av^3\]

where \(P\) is power in Watts (joules/second), \(\rho\) is the air density (kg/m³), \(A\) is the area covered by the turbine blades (square meters), and \(v\) is the wind velocity (m/s).

However, the Betz Limit means that turbines can only collect ~60% of the total wind power, which updates the theoretical “collectable” power (before accounting for inefficiencies, losses, etc.) to:

\[P = 0.3\rho Av^3\]

Write a function to calculate maximum collectable wind power (Watts) by a turbine requiring three inputs:

Air density (in kg/m³)
Rotor radius (in meters)
Wind velocity (in m/s)

Add the following errors and warnings:

A warning if the windspeed entered is > 130 (m/s)
A warning if the air density is > 1.225 kg / m³ (air density at sea level)
An error if the rotor radius is < 0

calc_windpower <- function(rho, radius, windspeed) {
  
  if (windspeed > 130) {
    warning("Whoa, that's a high windspeed! Are you sure that's correct?")
  }
  
  if (rho > 1.225) {
    warning("That air density is suspicious.")
  }
  
  if (radius < 0) {
    stop("Rotor radius must be a positive value (meters).")
  }
  
  0.3*rho*pi*(radius^2)*(windspeed^3)
  
}

Now test your function with different inputs. Are your messages working?

7. A few more interesting functions

Pulling values from a data frame example

# Let's create a data frame:


# Now let's write a function that automatically switches depth based on
gw_rate <- function(site) {
  
  # Stored parameters for 4 different sites
  gw_depths <- data.frame(sitename = c("mountain", "prairie", "desert", "beach"),
                 depth = c(32, 41, 63, 2),
                 slope = c(11.2, 0.4, 0.8, 2.6))
  
  # Subset for just that site information (creates a 1-row data frame)
  site_select <- filter(gw_depths, sitename == site)
  
  # Calculate using values from that 1-row data frame
  transport_rate <- 1.4 * site_select$slope + 3.6 * site_select$depth
 
  # Return the output
  return(transport_rate)
  
}

gw_rate(site = "beach")

[1] 10.84

# Alternatively, with switch()

gw_rate_switch <- function(site) {
  
  # Stored parameters for 4 different sites
  gw_depths <- switch(site, 
                      "mountain" = c(32, 11.2),
                      "prairie" = c(41, 0.4),
                      "desert" = c(63, 0.8),
                      "beach" = c(2, 2.6))
  
  # Calculate using values from that 1-row data frame
  transport_rate <- 1.4 * gw_depths[2] + 3.6 * gw_depths[1]
 
  # Return the output
  return(transport_rate)
  
}


gw_rate_switch("beach")

[1] 10.84

Logistic growth example

Logistic growth equation (within a for loop where growth rate changes)
Sinusoidal function with varying parameters

Logistic growth equation

In EDS 212, we learned about the logistic growth equation:

\[N_t=\frac{K}{1+[\frac{K-N_0}{N_0}]e^{-rt}}\]

Where \(N_0\) is the initial population size at time (\(t\)) 0, \(K\) is the carrying capacity, \(r\) is the population growth rate, and \(N_t\) is the population size at time \(t\).

First, let’s write write the bare-bones function:

# Build & check the minimum function
logistic_growth <- function(N0, K, r, time) {
  Nt <- K / (1 + ((K - N0) / N0) * exp(-r * time))
  print(Nt)
}

# Do the values check out when you test this? 
logistic_growth(N0 = 100, K = 6000, r = 0.27, time = 40)

[1] 5992.787

Cool. So this seems to be working when we assign single values for the different parameters.

Now, let’s explore what this looks like over a whole sequence of times (e.g. from t = 0 to t = 40):

# Create a vector of times:
time_vec <- seq(from = 0, to = 35, by = 0.1)

# Apply the logistic growth function to that vector of times (& store):
pop_35 <- logistic_growth(N0 = 100, K = 6000, r = 0.27, time = time_vec)

# Bind together the time_vec and population:
pop_time_35 <- data.frame(time_vec, pop_35)

# Always take a look at it
# View(pop_time_35)

# Alternatively with an inner for loop: 
pop_35_vec <- vector(mode = "numeric", length = length(time_vec))

for(i in seq_along(time_vec)) {
  population <- logistic_growth(N0 = 100, K = 6000, r = 0.27, time = time_vec[i])
  pop_35_vec[i] <- population
}

Now, a graph of the output:

# Make a little graph: 
ggplot(data = pop_time_35, aes(x = time_vec, y = pop_35)) +
  geom_line(size = 0.5)

Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.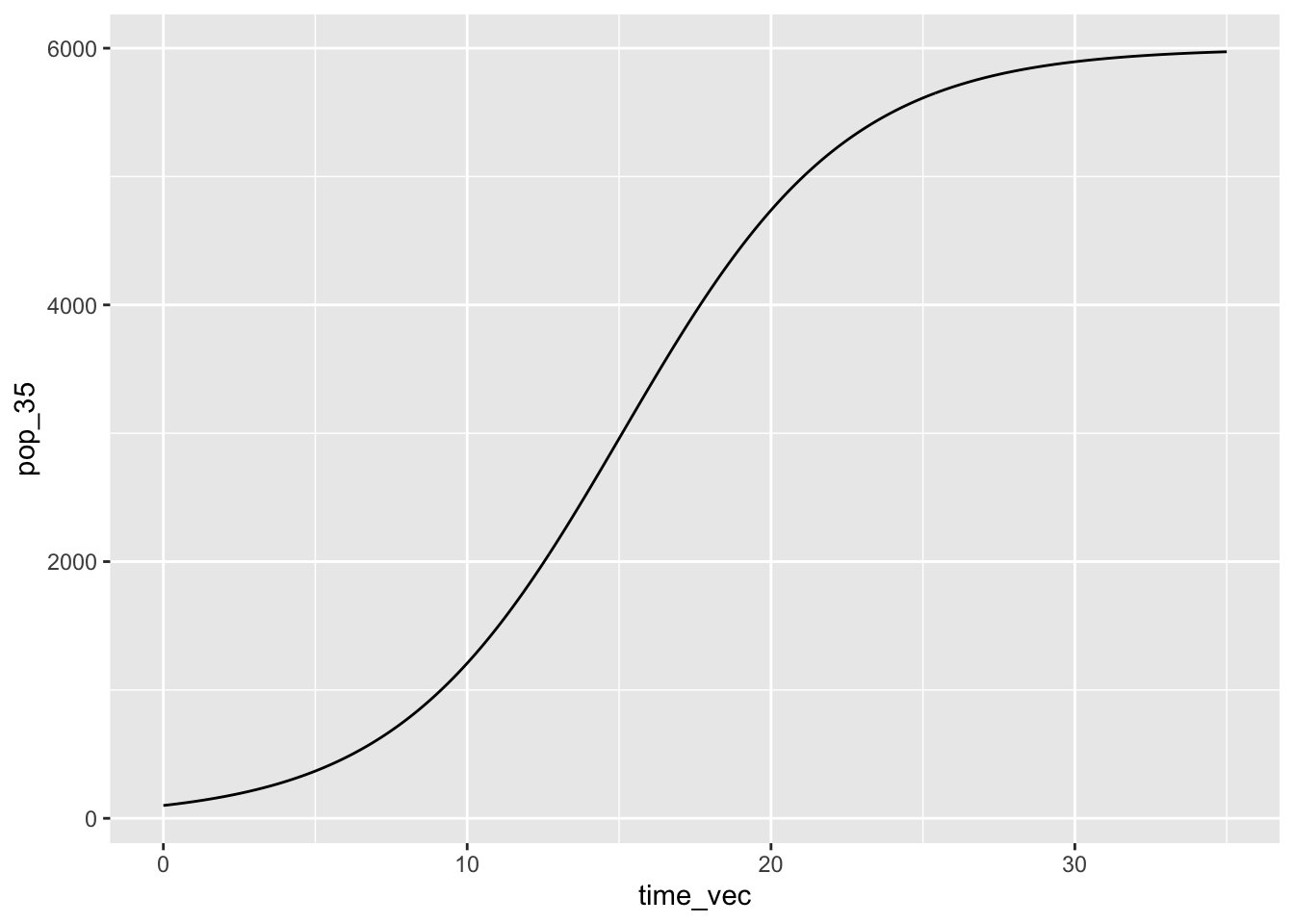

But we can imagine that we may want to ask: What does this look like as we change the initial population size? Or the growth rate? Etc.

In that case, we may want to apply our function over a range of growth rates (from 0.20 to 0.40, by increments of 0.01), for the time sequence we used here (0 to 35).

# Create a sequence of growth rate values: 
r_seq <- seq(from = 0.20, to = 0.40, by = 0.01)

Create a nested for loop!

# Create a for loop that goes through each, apply the 
# logistic growth function for a range of times for each growth rate

# Need to create a MATRIX to store the outputs in: 
out_matrix <- matrix(nrow = length(time_vec), ncol = length(r_seq))

# Now, a nested for loop:
for (i in seq_along(r_seq)) { # Outer loop is the growth rates
  for (j in seq_along(time_vec)) { # Inner loop is the time sequence values
  pop <- logistic_growth(N0 = 100, K = 6000, r = r_seq[i], time = time_vec[j])
  out_matrix[j, i] <- pop # Store the value in the appropriate row & column
  } 
}

Now some wrangling so we can visualize it:

# Let's wrangling it a little bit 
out_df <- data.frame(out_matrix, time = time_vec) # Make it a data frame and add time

# Update the column names of out_df, keeping time column name the same
colnames(out_df) <- c(paste0("gr_", r_seq), "time")

# pivot_longer to make it tidy (you'll learn more about this next week)
out_df_long <- out_df %>% 
  pivot_longer(cols = -time, names_to = "growth_rate", values_to = "population")

# Then plot it: 
ggplot(data = out_df_long, aes(x = time, y = population)) +
  geom_line(aes(color = growth_rate)) +
  theme_minimal()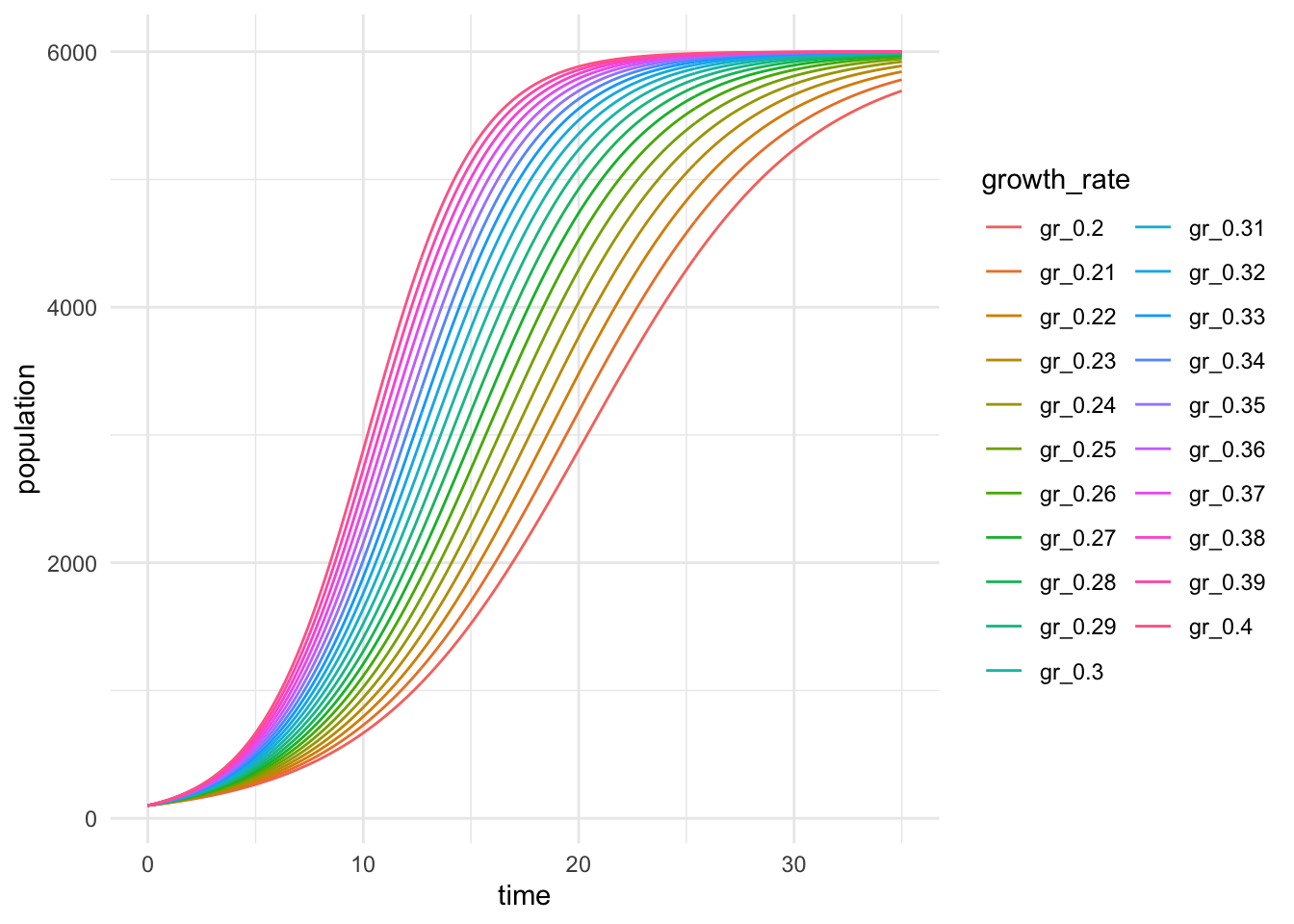

8. Testing functions with `{testthat}`

As we develop algorithms, we’ll change our code. We want a way to automatically check our function to make sure it’s behaving as expected. The testthat package “tries to make testing as fun as possible.”

Unit test: A unit test is an automated check of a piece (“unit”) of your code

Let’s consider an example. We’re writing a function to find the mean value of each column, then return the lowest and highest mean calculated (in that order). We would expect:

The outcome to be a numeric vector of length 2
Where the first value in the vector is smaller than the second value in that vector

Let’s write the function, then some accompanying tests to make sure they’re working.

mean_range <- function(df) {
  col_means <- map_df(df, .f = mean) # Returns column means as a df
  col_mean_max <- max(col_means) # Looks for the maximum value
  col_mean_min <- min(col_means) # Looks for the minimum value
  print(c(col_mean_min, col_mean_max))
}

# Try it out:
mean_range(df = mtcars)

[1]   0.40625 230.72188

OK great. But we’re doing some work on this code, and we don’t want to have to try a bunch of different things manually each time we change it to see how it breaks. Instead, we’ll write some automated tests for this function that help us avoid that (tomorrow!).

End Interactive Session 4

Extra examples

What’s the output of this nested for loop?

apples <- c(1, 2, 3, 4)
price <- c(7, 10, 25)

fruit_out <- matrix(nrow = length(price), ncol = length(apples))

for (i in seq_along(apples)) {
  for (j in seq_along(price)) {
    total_cost <- price[j] * apples[i]
    fruit_out[j, i] <- total_cost
  }
}

fruit_out

     [,1] [,2] [,3] [,4]
[1,]    7   14   21   28
[2,]   10   20   30   40
[3,]   25   50   75  100

file_prefix <- c("temp", "ph", "salinity")
file_suffix <- c(1, 2, 3, 4, 5)

# First: printing names
for (i in seq_along(file_prefix)) {
  for (j in seq_along(file_suffix)) {
    print(paste0(file_prefix[i], "_", file_suffix[j]))
  }
}

[1] "temp_1"
[1] "temp_2"
[1] "temp_3"
[1] "temp_4"
[1] "temp_5"
[1] "ph_1"
[1] "ph_2"
[1] "ph_3"
[1] "ph_4"
[1] "ph_5"
[1] "salinity_1"
[1] "salinity_2"
[1] "salinity_3"
[1] "salinity_4"
[1] "salinity_5"

# Second: storing them in a matrix (populated by COLUMN)
filename_matrix <- matrix(nrow = length(file_suffix), ncol = length(file_prefix))

for (i in seq_along(file_prefix)) {
  for (j in seq_along(file_suffix)) {
    file_name <- paste0(file_prefix[i], "_", file_suffix[j])
    filename_matrix[j, i] <- file_name
  }
}

filename_matrix

     [,1]     [,2]   [,3]        
[1,] "temp_1" "ph_1" "salinity_1"
[2,] "temp_2" "ph_2" "salinity_2"
[3,] "temp_3" "ph_3" "salinity_3"
[4,] "temp_4" "ph_4" "salinity_4"
[5,] "temp_5" "ph_5" "salinity_5"

Another for loop example:

quarter_splits <- c(1, 1.1, 1.2, 1.1, 1.4, 1.5, 1.6, 1.4)

half_splits <- vector(mode = "numeric", length = length(quarter_splits) - 1)

# NOTE FOR CLASS OF 2023: check seq_along here, use 1:(length(quarter_splits) - 1) instead
for (i in 1:(length(quarter_splits) - 1)) {
  half_mile <- quarter_splits[i] + quarter_splits[i + 1]
  half_splits[i] <- half_mile
}

half_splits

[1] 2.1 2.3 2.3 2.5 2.9 3.1 3.0

dosage <- c(10, 100, 1000)

dose_index <- vector(mode = "character", length = length(dosage))

for (i in seq_along(dosage)) {
  k <- paste0("zinc_", dosage[i])
  dose_index[i] <- k
}

dose_index

[1] "zinc_10"   "zinc_100"  "zinc_1000"

odds <- c(1, 3, 5)
evens <- c(2, 4, 6, 8)

for (i in seq_along(odds)) {
  for (j in seq_along(evens)) {
    print(odds[i] * evens[j])
  }
}

[1] 2
[1] 4
[1] 6
[1] 8
[1] 6
[1] 12
[1] 18
[1] 24
[1] 10
[1] 20
[1] 30
[1] 40

1. Learning from existing functions

Function documentation

In R…

In Python…

2. Basic pieces of a function

Components of a function

3. Getting started - function examples in R & Python

Example 1 (from lecture slides)

Example 2

Example 3

print() versus return()

Example 4

4. Functions with conditionals

Example

Example

5. Functions meet for loops

Example

6. Adding helpful error and warning messages

Adding error messages with conditional checks + stop()

Adding warning messages

7. A few more interesting functions

Pulling values from a data frame example

Logistic growth example

Logistic growth equation

8. Testing functions with {testthat}

Another for loop example:

`print()` versus `return()`

Adding error messages with conditional checks + `stop()`

8. Testing functions with `{testthat}`